1. 1bit全加器
1bit全加器电路结构如下所示,其中,a和b为相加的数,而cin为进位输入,s为本位加的结果,cout为进位输出。

可以用下面组合逻辑代码写1bit全加器。
module 1bit_adder (
input a ,
input b ,
input cin ,
output s ,
output cout
);
wire p ;
wire g ;
assign p = a | b ;
assign g = a & b ;
assign s = a ^ b ^ cin ;
assign cout = (p & cin) | g ;
endmodule
其中p为进位传递,若cin为1,并且a、b中有一个为1,那么p将cin进位传递到进位输出;g为产生进位,是a和b加的过程中产生的进位,那就是a和b都为1情况下。当a、b和cin中有奇数个1时,本位计算结果s就为1,可用异或逻辑。这种方法在后面超前进位加法器中也用到了。
在Vivado中综合出的电路如下图。

或者直接通过下面代码写全加器。
module gold_adder_1bit(
input a ,
input b ,
input cin ,
output cout,
output sum
);
assign {cout, sum} = a + b + cin ;
endmodule
Vivado综合工具会自动优化,上述代码综合出的电路如下。

将上述用组合逻辑搭建的超前进位加法器作为测试,而将直接综合成加法器的代码作为gold模块。通过特殊情况赋值和随机产生方式,生成测试激励,将测试结果与gold生成的结果比对,如果出现错误,自动停止,对应的testbench代码如下:
module adder_1bit_tb(
);
reg a ;
reg b ;
reg cin ;
wire test_s ;
wire test_cout;
wire gold_sum ;
wire gold_cout;
reg clk ;
always #5 clk = ~clk ;
integer i ;
initial begin
clk = 0 ;
a = 0 ; b = 0 ; cin = 0 ;
repeat(3) @ (posedge clk) ;
a = 1 ; b = 1 ; cin = 0 ;
repeat(3) @ (posedge clk) ;
a = 1 ; b = 0 ; cin = 1 ;
repeat(3) @ (posedge clk) ;
a = 0 ; b = 1 ; cin = 1 ;
repeat(3) @ (posedge clk) ;
a = 1 ; b = 1 ; cin = 1 ;
repeat(3) @ (posedge clk) ;
for (i = 0 ; i<= 100 ; i = i+1) begin
a = $random();
b = $random();
cin = $random();
@ (posedge clk) ;
end
#20 ;
$stop ;
end
reg test_error = 0 ;
always @(posedge clk ) begin
#1 ;
if((test_s != gold_sum) || (test_cout != gold_cout)) begin
test_error <= 1'b1 ;
#10;
$stop ;
end
end
adder_1bit u_adder_1bit (
.a (a ) ,
.b (b ) ,
.cin (cin ) ,
.s (test_s ) ,
.cout (test_cout)
);
gold_adder_1bit u_gold_adder_1bit (
.a (a ) ,
.b (b ) ,
.cin (cin ) ,
.sum (gold_sum ) ,
.cout (gold_cout)
);
endmodule
2. 行波进位加法器(Ripple Adder)
可以通过1bit全加器搭建8bit全加器,将每个bit都使用全加器加,将进位串行,这种1bit级联起来的加法器也叫行波进位加法器。与我们手工算一个加法一样,先算低位,再算高位。

可直接用1bit行波进位方法搭,verilog代码如下,也可直接把1bit行波进位加法器例化为子模块,例化8个子模块。
module adder_8bit(
input [7:0] a ,
input [7:0] b ,
input cin ,
output [7:0] sum ,
output cout
);
wire [7:0] p ;
wire [7:0] g ;
wire [7:0] c ;
assign c[0] = cin ;
assign p[0] = a[0] | b[0] ;
assign g[0] = a[0] & b[0] ;
assign sum[0] = a[0] ^ b[0] ^ c[0] ;
assign c[1] = (p[0] & c[0]) | g[0] ;
assign p[1] = a[1] | b[1] ;
assign g[1] = a[1] & b[1] ;
assign sum[1] = a[1] ^ b[1] ^ c[1] ;
assign c[2] = (p[1] & c[1]) | g[1] ;
assign p[2] = a[2] | b[2] ;
assign g[2] = a[2] & b[2] ;
assign sum[2] = a[2] ^ b[2] ^ c[2] ;
assign c[3] = (p[2] & c[2]) | g[2] ;
assign p[3] = a[3] | b[3] ;
assign g[3] = a[3] & b[3] ;
assign sum[3] = a[3] ^ b[3] ^ c[3] ;
assign c[4] = (p[3] & c[3]) | g[3] ;
assign p[4] = a[4] | b[4] ;
assign g[4] = a[4] & b[4] ;
assign sum[4] = a[4] ^ b[4] ^ c[4] ;
assign c[5] = (p[4] & c[4]) | g[4] ;
assign p[5] = a[5] | b[5] ;
assign g[5] = a[5] & b[5] ;
assign sum[5] = a[5] ^ b[5] ^ c[5] ;
assign c[6] = (p[5] & c[5]) | g[5] ;
assign p[6] = a[6] | b[6] ;
assign g[6] = a[6] & b[6] ;
assign sum[6] = a[6] ^ b[6] ^ c[6] ;
assign c[7] = (p[6] & c[6]) | g[6] ;
assign p[7] = a[7] | b[7] ;
assign g[7] = a[7] & b[7] ;
assign sum[7] = a[7] ^ b[7] ^ c[7] ;
assign cout = (p[7] & c[7]) | g[7] ;
endmodule
综合结果如下,可以看到这种通过1bit级联方法搭建的8bit加法器,延时会很大,因为必须算完低bit位才能算高bit位。因此,这种形式的加法器性能很差。

将上述8bit行波进位加法器作为测试,而将直接综合成8bit加法器的代码作为gold模块。通过随机产生方式,生成测试激励,将测试结果与gold生成的结果比对,如果出现错误,自动停止,对应的testbench代码如下:
module adder_8bit_tb(
);
reg [7:0] a ;
reg [7:0] b ;
reg cin ;
wire [7:0] test_s ;
wire test_cout ;
wire [7:0] gold_sum ;
wire gold_cout ;
reg clk ;
always #5 clk = ~clk ;
integer i ;
initial begin
clk = 0 ;
a = 0 ; b = 0 ; cin = 0 ;
for (i = 0 ; i<= 1000 ; i = i+1) begin
if(i<=200) begin
a = a + 1 ;
b = b + 3 ;
cin = $random ;
end
else if(i<=400) begin
a = a + 2 ;
b = b + 1 ;
cin = $random ;
end
else begin
a = $random();
b = $random();
cin = $random();
end
@ (posedge clk) ;
end
#20 ;
$stop ;
end
reg test_error = 0 ;
always @(posedge clk ) begin
#1 ;
if((test_s != gold_sum) || (test_cout != gold_cout)) begin
test_error <= 1'b1 ;
$display("ERROR!!!") ;
#10;
$stop ;
end
end
adder_8bit u_adder_8bit (
.a (a ) ,
.b (b ) ,
.cin (cin ) ,
.sum (test_s ) ,
.cout (test_cout)
);
gold_adder_8bit u_gold_adder_8bit (
.a (a ) ,
.b (b ) ,
.cin (cin ) ,
.sum (gold_sum ) ,
.cout (gold_cout)
);
endmodule
其中,gold_adder_8bit模块代码如下:
module gold_adder_8bit(
input [7:0] a ,
input [7:0] b ,
input cin ,
output cout,
output [7:0] sum
);
assign {cout, sum} = a + b + cin ;
endmodule
3. Carry-Select Adder
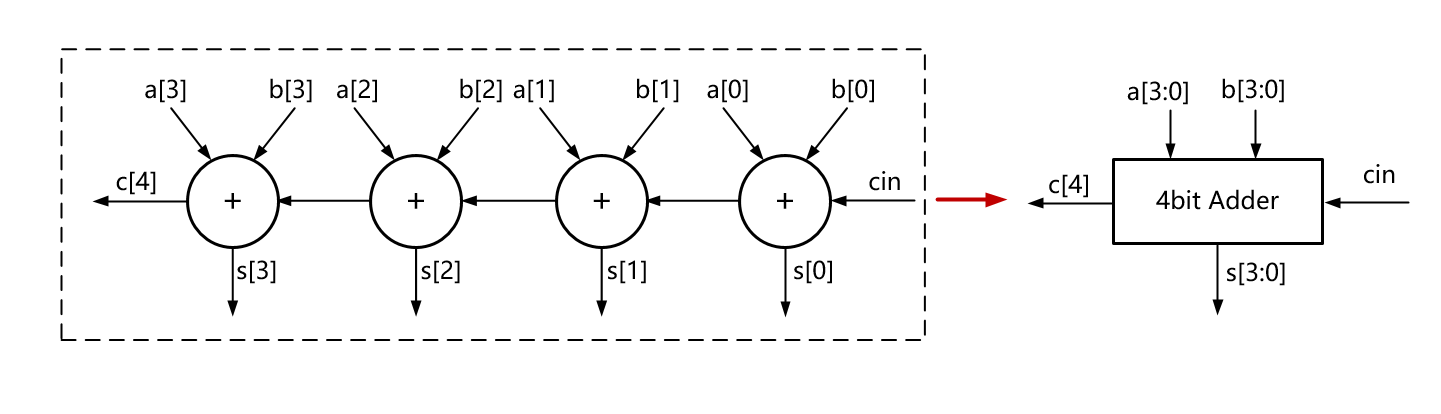
既然行波进位加法器延时大,那么可以通过下面方法进行电路结构上的优化。如下图所示,首先定义一个4bit的行波进位加法器,将这个4bit行波进位加法器封装起来,以这个4bit加法器去优化更高bit的加法器。
Carry-Select Adder优化电路如下图所示,以8bit加法为例,低位4bit按照封装的加法器运算,但是对高位4bit来说,将低位进位为0和1的情况都计算了一遍,因为c[4]不上为0就是为1,那么可以不管低位4bit有没有产生进位输出,将高位4bit在c[4]为0和1的情况都进行加法运算,然后依据c[4]的结果对高位4bit的sum和cout都进行选择。
这种方法可以看到3各4bit加法器都是并行运算的,可以同时进行运算,运算后通过c[4]结果选择高位4bit的sum和cout。就不用像行波进位加法器那样必须得等低bit的进位,高bit才能开始运算。

Carry-Select Adder 8bit加法器设计代码如下,其中Ripple_Adder_4bit为4bit输入的行波进位加法器。
module Carry_Select_Adder(
input [7:0] a ,
input [7:0] b ,
input cin ,
output [7:0] sum ,
output cout
);
wire c4 ;
wire [3:0] sum7_4_0 ;
wire c8_0 ;
wire [3:0] sum7_4_1 ;
wire c8_1 ;
assign sum[7:4] = (c4==1) ? sum7_4_1 : sum7_4_0 ;
assign cout = (c4==1) ? c8_1 : c8_0 ;
Ripple_Adder_4bit u0_Ripple_Adder_4bit (
.a (a[3:0] ) ,
.b (b[3:0] ) ,
.cin (cin ) ,
.sum (sum[3:0] ) ,
.cout (c4 )
);
Ripple_Adder_4bit u1_Ripple_Adder_4bit (
.a (a[7:4] ) ,
.b (b[7:4] ) ,
.cin (1'b0 ) ,
.sum (sum7_4_0 ) ,
.cout (c8_0 )
);
Ripple_Adder_4bit u2_Ripple_Adder_4bit (
.a (a[7:4] ) ,
.b (b[7:4] ) ,
.cin (1'b1 ) ,
.sum (sum7_4_1 ) ,
.cout (c8_1 )
);
endmodule
Vivado综合出来的电路结果如下图所示。






