1. 超前进位加法器
与1bit全加器方法类似,生成信号为两数单bit与,传播信号为两数单bit或,进位则可以用如下表示。超前进位加法器相当于在算法上进行优化。

各bit进位表示如下,对于一个4bit加法器来说,最终需要得到的是C4,而C1,C2,C3,C4都可以用G、P、C0这些已知参数计算。并不需要等待低bit运算完的进位,这样就能增加并行性,从而减小加法运算延时,但是也使得电路面积增大。这种方法叫做超前进位加法器(Carry-Look ahead Adder,CLA)。

4bit超前进位加法器器综合出来的电路如下如所示,可以看到相比于行波进位加法器,其关键路径减少,布线延时和逻辑延时都会降低。

4bit超前进位加法器代码如下:
module CLA_Adder(
input [3:0] a ,
input [3:0] b ,
input cin ,
output [3:0] sum ,
output cout
);
wire [3:0] g , p , c ;
assign g = a & b ;
assign p = a | b ;
assign c[0] = cin ;
assign c[1] = g[0] | (p[0] & c[0]) ;
assign c[2] = g[1] | (p[1] & (g[0] | (p[0] & c[0]))) ;
assign c[3] = g[2] | (p[2] & (g[1] | (p[1] & (g[0] | (p[0] & c[0]))))) ;
assign cout = g[3] | (p[3] & (g[2] | (p[2] & (g[1] | (p[1] & (g[0] | (p[0] & c[0])))))));
assign sum = a ^ b ^ c ;
endmodule
2. 进位保留加法器
进位保留加法器(Carry Save Adder,CSA)在执行多个数加法时具有极小的进位传播延迟,假设三个数相加,一般方法是先将前两个数相加,结果再与第三个数相加,而进位保留加法器的基本思想是将进位c和本位计算结果s分别保存,并且在计算时每个bit同时进行计算c和s。
假设4bit三个数如下图所示,进位保留加法器计算时,第一,先进行本位sum计算,即三个数对应bit位相加,如果有奇数个1,则sum为1,偶数个1,sum为0。第二,计算进位Carry,低位向高位进位,三个数对应bit中只要出现2个以上的1,就会产生进位,并且进位要比原来bit高1位。第三,将Carry低位补个0,sum高位补个0,使得二者位数相等,进行加法运算。

上述计算方法在电路中结构如下图所示,3个数,每个对应bit都同时并行进行加法运算,然后将c和s的结果拼接、位数补齐(c低位补0,s高位补0),再将c和s进行一次加法运算。

Vivado综合结果如下,电路delay为1个1bit加法器的delay(4个并行)+最后1个5bit加法器delay,远小于串行方式delay。CSA简化操作可以看成是在真正进行两个数加法之前的预处理操作。

进位保留加法器RTL代码如下:
module CSA_4bit(
input [3:0] num1 ,
input [3:0] num2 ,
input [3:0] num3 ,
output cout,
output [4:0] sum
);
wire [4:0] c ;
wire [4:0] s ;
assign c[0] = 1'b0 ;
assign s[4] = 1'b0 ;
assign {cout,sum} = s + c ;
adder_1bit u0_adder_1bit (
.a (num1[0] ) ,
.b (num2[0] ) ,
.cin (num3[0] ) ,
.s (s[0] ) ,
.cout (c[1] )
);
adder_1bit u1_adder_1bit (
.a (num1[1] ) ,
.b (num2[1] ) ,
.cin (num3[1] ) ,
.s (s[1] ) ,
.cout (c[2] )
);
adder_1bit u2_adder_1bit (
.a (num1[2] ) ,
.b (num2[2] ) ,
.cin (num3[2] ) ,
.s (s[2] ) ,
.cout (c[3] )
);
adder_1bit u3_adder_1bit (
.a (num1[3] ) ,
.b (num2[3] ) ,
.cin (num3[3] ) ,
.s (s[3] ) ,
.cout (c[4] )
);
endmodule
其中adder_1bit为1bit的全加器,RTL代码如下:
module adder_1bit(
input a ,
input b ,
input cin ,
output s ,
output cout
);
wire p ;
wire g ;
assign p = a | b ;
assign g = a & b ;
assign s = a ^ b ^ cin ;
assign cout = (p & cin) | g ;
endmodule
3. Wallace Tree
Wallace Tree可以看作是CSA的扩展,当有多个数相加时,可不断将三个数进行CSA操作,CSA进3个数,出carry和sum(2个数),和另一个CSA的结果组成三个数,再CSA操作,直到最终通过CSA简化成两个数,将这两个数通过加法器相加即可。
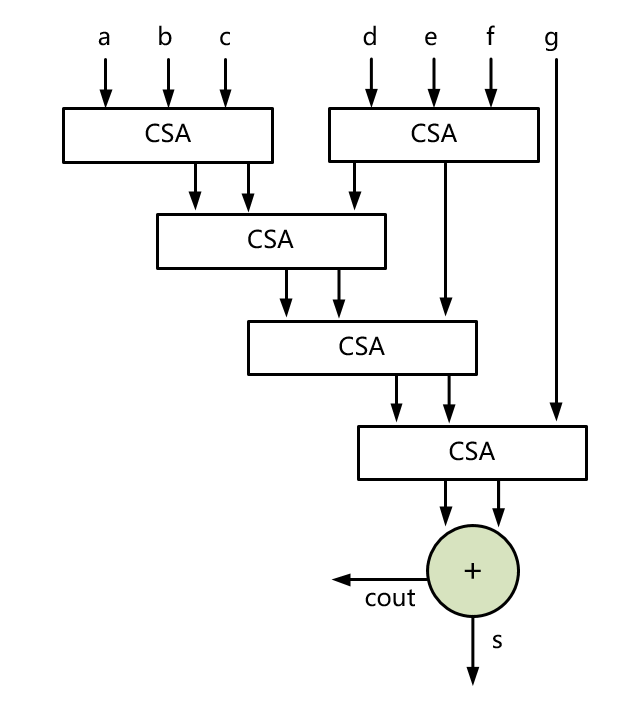
对于Wallace Tree结构,在进行多个数加法时,还可以使用流水线结构,可以在某个CSA之间插入寄存器,形成流水处理,这样对提升主频将会有更大的帮助。
参考资料
[1].https://www.jianshu.com/p/6ce9cad8b467
[2].https://blog.csdn.net/zhouxuanyuye/article/details/103947258
[3].https://blog.csdn.net/qq_40677883/article/details/128961549





