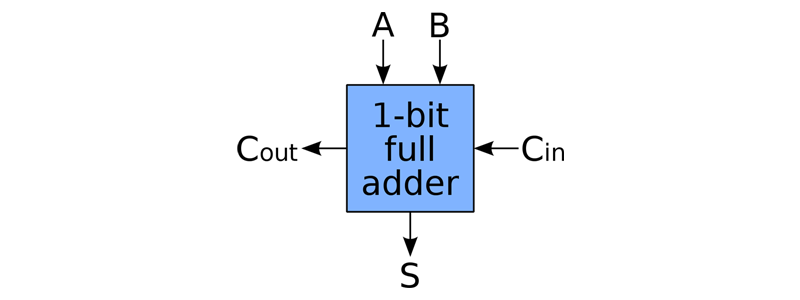
手动乘法过程如下,用乘数的每一个bit分别去乘被乘数,最后将所有的中间结果相加就可以得到结果。

若是M×N-bit乘法,则为N的每个bit去乘M,得到N个M-bit的partial products,将N个partial products累加就是乘法结果。N个数累加可以用Wallace Tree结构运算。
1. Radix-4 Booth乘法器
通过每个bit去乘的这种方法,如果乘数位宽高,就会产生较多个partial products,为了减少Wallace Tree结构的层数,可以通过每2bit去分别乘。
假设被乘数为Y,将1bit编码改变为2bit编码,2bit编码如下。比如b1=1,b0=0时,可以看成2乘Y。
| b1 | b0 | partial | partial |
|---|---|---|---|
| 0 | 0 | 0Y | 0Y |
| 0 | 1 | 1Y | 1Y |
| 1 | 0 | 2Y | 4Y-2Y |
| 1 | 1 | 3Y | 4Y-Y |
在电路中1Y容易,2Y就是将Y左移1位,4Y就是将Y左移2位。即4Y={Y,2'b00},2Y={1'b0,Y,1'b0}。-Y也比较好做,-Y就是将Y取反再加1,-2Y就是将2Y取反加1。比如Y=6'b001100,那么-Y=6'b110100,2Y=6'b011000,-2Y=6'b101000。
将上面partial改写,可将3Y改成4Y-Y,2Y改成4Y-Y。4Y表示权重升高,因为b1b0最多可以表示2’b11,而4Y为100,可以看成对下一组{b3,b2}编码的进位。经过变换之后,本位只留下0Y、1Y、-2Y、-Y部分积,本位部分积从原来的2个变为1个。
{b1,b0}编码的进位b_cin和下一组编码{b3,b2}的编码对应如下,比如b3=1,b2=0,应该为2Y,且b cin为0,没有进位,所以其对应的部分积(partial products)为2Y,写成4Y-2Y;b3=1,b2=0,为2Y,且b cin为1,有进位,所以为3Y,写成4Y-Y。
| b3 | b2 | b_cin | partial |
|---|---|---|---|
| 0 | 0 | 0 | 0Y |
| 0 | 1 | 0 | 1Y |
| 1 | 0 | 0 | 4Y-2Y |
| 1 | 1 | 0 | 4Y-Y |
| 0 | 0 | 1 | 1Y |
| 0 | 1 | 1 | 2Y |
| 1 | 0 | 1 | 4Y-Y |
| 1 | 1 | 1 | 4Y |
通过上述完整的Radix-4编码表可以发现,当b3为1时,出现了4Y,也就是产生了进位,其他情况没有向下一组编码的进位。
比如做16bit乘法,最右侧表示第一次进位固定为0,重叠部分如b1表示有进位产生,所以Radix-4编码后有9个partial,如果1bit分别乘的话就会有16个partial,因此,较少了partial的数量,也就减少了Wallace Tree的向下级数。
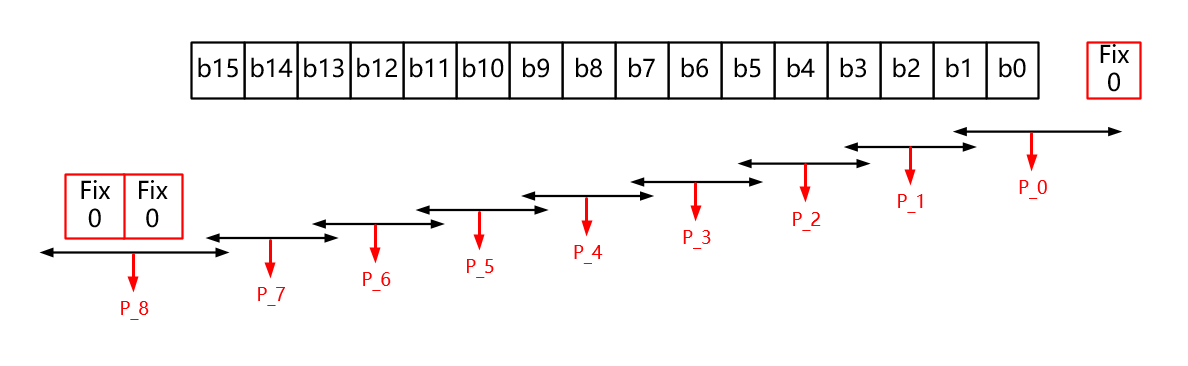
假设A×B,B=11(十进制),其二进制为4'b1011,在其最低位补0,高位补2个符号位,其编码就如下图。

像Wallace Tree这些,在真正实现的时候,直接用*即可,不论是DC还是Vivado,综合工具都会自动综合为这些结构。
当我们需要更高的频率的时候,由于追求频率,可能会导致一个cycle做不完,即输入后需要等待几个cycle才能出结果,这时候需要带有流水线结构的乘法器IP来做,DC和Vivado中也提供了IP。
我们可以不用研究乘法器IP的结构,直接调用,但是上述这些知识需要知道,这样就能知道大概的delay,心里有个数,很多经验丰富的芯片工程师在设计时都会预估项目工程的delay,以预计可达到的主频,从而做到心里有数。