按照前面数字IP设计流程。
1. 设计需求
设计1个bin2BCD简单IP,BCD编码为二进制表示的十进制编码。设计一个11位的有符号二进制数(取值范围[-1023,1023])到17bit的BCD码(10进制编码),17bitBCD编码定义如下。
| Bit | 说明 |
|---|---|
| 16 | 表示符号位,0是正数,1是负数 |
| 15:12 | 千位的BCD码,取值为十六进制显示的0~9 |
| 11:8 | 百位的BCD码,取值为十六进制显示的0~9 |
| 7:4 | 十位的BCD码,取值为十六进制显示的0~9 |
| 3:0 | 个位的BCD码,取值为十六进制显示的0~9 |
比如输入11'h020(正32),输出17'h00032;输入11'h79C(负100),输出17'h10100。
首先对于无符号数和有符号数,可表示数的范围也是不一样的,比如都为5bit数来说,无符号数的取值范围为十进制的[0,31],那有符号数的取值范围为十进制的[-16,15],因为无符号数没有符号位,5bit全是数值位,而有符号数最高1bit是符号位,只有4bit的数值位。
在计算机中,数值都是统一以补码的形式计算和存储的。对于无符号数,补码与原码相同;对于有符号数,补码的最高位仍为符号位,正数的补码与原码相同,而负数的补码为原码的反码加1,负数的原码也等于其补码取反加1。
比如+32为有符号正数,其补码为11'b000_0010_0000即11'h020,等于其原码,其中最高位0为符号位。-100为有符号负数,其原码为11'b100_0110_0100,反码为11'b111_1001_1011,补码为11'b111_1001_1100,即11'h79C。
-100(十进制),11bit有符号数计算位为10bit,2^10=1024,1024-100=924(十进制),924即为补码计算位的十进制数,924(10)=10'h39C(16),算上最高位为1的符号位,-100(10)=11'h79C(16)。
2. 算法分析
2.1 查找表法
2.1.1 算法描述
通过设计需求分析阶段的解读,可以发现bin的取值范围是[-1023,1023],并且每一个输入bin对应一个输出BCD码,所以二者具有线性关系。可以使用查找表的方法进行设计。
可以将取值范围对应的BCD码存入RAM/ROM中,以bin的输入作为地址,根据地址去查找对应的BCD码输出。因此,RAM的深度为2047,数据位宽为17bit。

为了减少RAM深度,再进一步分析发现,负数和正数的BCD编码除了符号位不同之外其他相同,比如-234(10)和234(10)的BCD编码不算符号位都为234(16),因此,可以对输入的bin加绝对值,再去查找BCD码,输出时正数直接输出,负数符号位写成1和绝对值的BCD码位宽组合起来输出。这样RAM的深度变为1024,数据位宽为16bit。
再优化,可以发现由于取值范围的限定,bin的千位不是0就是1,也就是又可以去掉千位的查表,对于判断是否千位为1,可以做一个1000比较器,当大于等于1000时,BCD千位为1,否则为0。这样RAM的深度为1024,位宽为12bit。
所以最终可以做一个1024*12bit的RAM进行查表。
2.1.2 性能分析
查找表法PPA分析来看,优点是电路结构简单,只使用RAM和一些组合逻辑即可,比较直观。缺点是RAM的深度和位宽会随着bin的位宽增大而增大,面积会增加,不利于bin位宽扩展。
2.2 除法
2.2.1 算法描述
上述设计需求就是给出一个11bit有符号数,去不断分解其个位、十位、百位、千位的过程。在C++学习时也有类似的方法,直接不断去除10,得到商和余数,余数就是这些。
比如-1021(10),绝对值后1021(10)。
1021/10=102,1021%10=1(个位);
102/10=10,102%10=2(十位);
10/10=1,10%10=0(百位);
1/10=0,1%10=1(千位)。
2.2.2 性能分析
除法方法需要用到除法和取余等计算,而除法本身计算周期较长,算的慢,因此,尽量避免使用除法。
2.3 穷举法
2.3.1 算法描述
穷举法就是从千位开始,不断进行比较、判断,直到结束。本设计中,千位只能为0或1,而百位可以为0,1,……9,其他类似。
比如bin为1021(10),1021≥1000,如果条件真,表示是一个大于或等于1000的数,那么千位为1,否则为0。执行完千位后,bin值变为021(10),即1021-1000。
021≥900,百位1,否则再判断是否≥800,百位为8,依次判断下去,直到找到合适的数值区间。
个位、十位类似。
2.3.2 性能分析
穷举法结构上看起来比较复杂,用到的电路器件为减法器和选择器。本实例使用穷举法。
3. 模块IO定义
整个设计模块IO接口定义如下。

| Name | I/O | Bits | Description |
|---|---|---|---|
| clk | I | 1 | 时钟输入 |
| rst_n | I | 1 | 同步复位输入,低有效 |
| bin | I | 11 | 11bit有符号数,二进制值,取值范围[-1023, 1023] |
| bin_vld | I | 1 | bin输入有效位,为1表示输入的bin有效 |
| bcd | O | 17 | BCD码输出 |
| bcd_vld | O | 1 | 为1表述BCD码输出有效 |
接口时序如下图所示,bin_vld电平可以任意变化,表示输入的bin有效。bin与bin_vld没有Delay。bin输入后间隔几个周期输出有效bcd。

4. Cycle级Pipeline
通常来说,大部分的处理过程都无法在一个周期内完成,基本都会分成几个步骤,比如先干这一步,这一步结束后再去干下一步,所以不用Pipeline时,这些过程基本都是串行进行下去的,这样做的效果就是输入后需要等待好几个周期才能有输出,在这期间无法再次输入,这会使得处理的吞吐率很低。
而加入流水线后,就以最理想的流水线(流水线无阻塞情况)来说,它可以在每个周期都能接收输入信号,并且几个周期过后能保证每个周期都能产生输出,所以流水线会大幅增加数据的吞吐率。
再假设全用组合逻辑做,保证每个周期都能算出来,这样吞吐率是提升了,可是全组合逻辑就会产生很大的Delay,这样时钟频率就上不去。
所以使用Pipeline有2个好处,第一是提高吞吐率,第二是提高时钟频率。
以四选一选择器为例,假设全组合逻辑,每个选择器Delay为10ns,那总共的Delay为20ns,频率为50MHz;而插入寄存器后,寄存器左侧和右侧各有10ns的延时,假设不考虑DFF的延时,频率就可以跑到100MHz了。
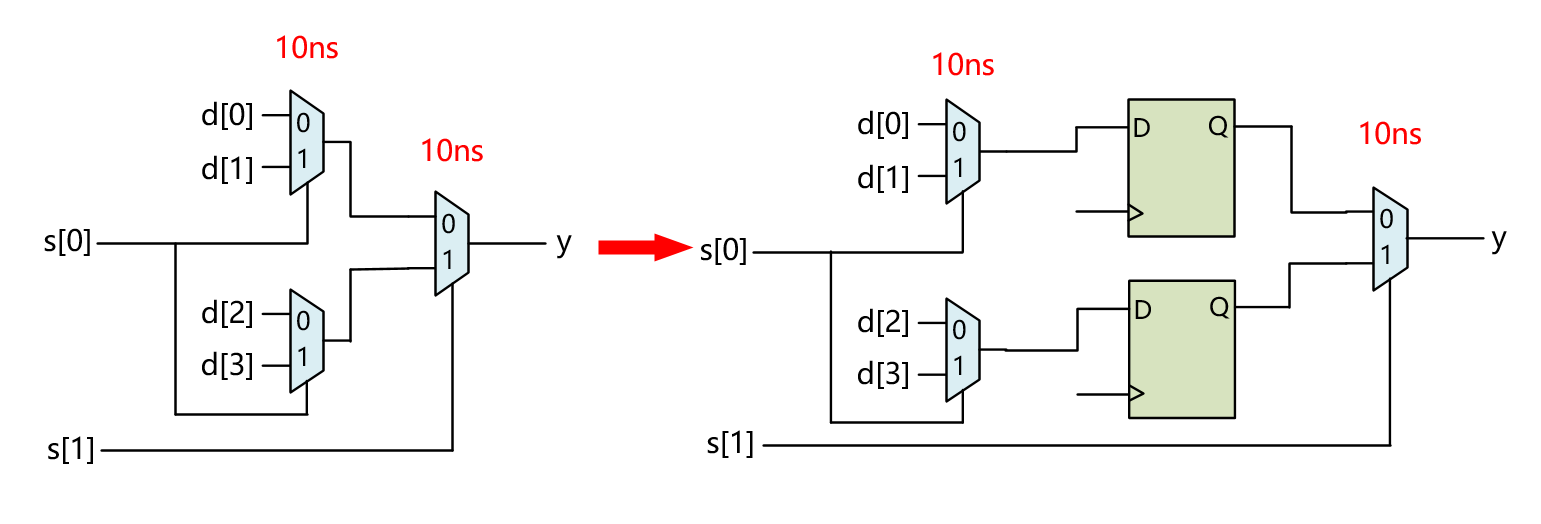
上图插入DFF构成Pipeline后的电路功能是有问题的。假如每个时钟周期s0,s1都发生变化,那么加入DFF后s0到达DFF输入时,s1已经到达了DFF右侧MUX,控制选择的是上一个Cycle DFF锁存的值,并不是当前Cycle s0的值,因为它还没有锁存到DFF中。
正确的带有DFF而形成Pipeline的电路结构如下图。

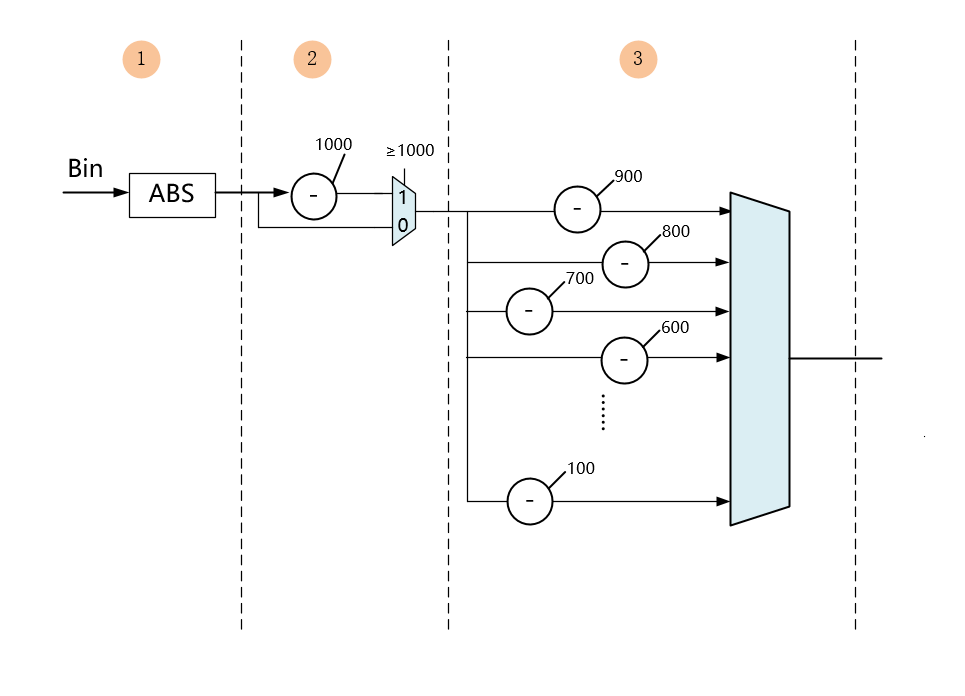
穷举法Pipeline电路结构如下,其中Cycle1主要是输入和ABS绝对值计算,Cycle2主要是计算千位BCD码,通过判断是否≥1000,若≥1000,千位BCD为1,且将减去1000的值向下级传递,否则为BCD码为0,将原值直接向下传递。
Cycle3为计算百位BCD码,九个减法器可并行计算,计算后通过带有优先级的选择器,输出百位的BCD码,并且将减去后的值传递到下一级。十位、个位计算电路结构与百位类似。虚线位置即为插入DFF的位置。
Cycle级流水线如下图,通过流水线设计,可以在每个cycle都能进入有效的bin值进行运算,并且在几个cycle之后,流水线完全运行起来之后,每个cycle都能输出bcd值。需要注意的是,每一级的输出都需要进行一级一级往下传递,直到bcd码的输出。

参考资料
[1].https://blog.csdn.net/qq_40677883/article/details/128997432





